

Mathematics of Convergent Fractals
Newton's Method
The fractals discussed in this section use complex numbers. See Mathematics of Divergent Fractals for a brief discussion on complex arithmetic. Newton's Method is an iterative method that can be used to solve a variety of equations that can be differentiated. To be differentiatable, the first derivative of the function must exist. For example, consider the equation
z3 - 1 = 0
This equation is simple enough to solve directly, even when z is a complex number. The roots are
r1 =
1
r2 = -1/2 + sqrt(3)/2i
r3 = -1/2 - sqrt(3)/2i
If these roots are plotted on graph paper with the X axis being the real axis and the Y axis being the imaginary axis, the roots will lie equally spaced on a circle of radius 1. For any differentiable function f(z) Newton's Method is:
zn+1 = zn - f(zn)/f '(zn)
where f '(z) is the derivative of f(z). With an initial guess close enough to a root of f(z), the sequence z0, z1, z2, z3... will converge on the value of the root. This root is called the attractor for the sequence. We will come back to this term in the section on the Mathematics of Strange Attractors. For the equation f(z) = z3 - 1 Newton's Method gives:
zn+1 = (2zn3 + 1)/(3 zn2)
For initial guesses for z0 which are sufficiently close to any of the roots, the sequence rapidly converges on the root. Something interesting happens, however, when the initial guess is about half way between any of the roots. This is illustrated in the images below. The three colors, yellow, green and blue, represent the starting points for convergence to the three roots. Images 2 and 3 are zooms into the starting image - this is the behavior of a self-similar fractal! Our Newton's Method iteration has generated a fractal image. Each color represents a basin of attraction for a given root of the equation. Although the root (1,0) is on the right hand side of the image, pieces of the basin can be found throughout the image.
| original image | 300 fold zoom | 100000 fold zoom |
From an artistic perspective, images would normally be generated by setting a "bailout", in this case a small number such as 0.000001. The points in the complex plane (the starting points for the Newton's Method iterations) would then be colored according to the number of iterations needed for the absolute value of the difference between zn and zn+1 to become smaller than the bailout value. The following image is a result of this process:

The image is banded, similar to what we saw for divergent fractals, which detracts from its artistic appeal. The formula developed by Ron Barnett in 1995 for divergent fractals also works with Newton' Method convergent fractals with a minor modification:
The original equation:
sn+1 = sn + e-||zn+1||
where ||zn+1|| is the absolute value of zn+1.
The modified equation:
sn+1 = sn + e-||wn+1||
where ||wn+1|| is the absolute value of 1/(zn - zn+1). The image below was generated with this coloring method:

Fractal artists have developed many coloring methods which depend upon various characteristics of the sequences generated by iteration of Newton's Method, and which provide extensive control of the type of image produced according to the artistic goals of the artist.
Now let's consider something slightly more complex than f(z) = z3 - 1.
Fractal images from f(z) = z3 - cz + c - 1
This is a really interesting equation. When Newton's Method is applied to it the following iterative equation is obtained:
zn+1 = (2zn3 - c + 1)/(3zn2 - c)
Start with a graph that runs from -2 to 2 on X, or real, axis and from -1.5 to 1.5 on the Y, or imaginary axis. For each point on the graph, assign the point to c and start the iteration with z0 = (0, 0). The image obtained, using Ron Barnett's smooth coloring method, doesn't look like anything special - until a zoom is made into the image:
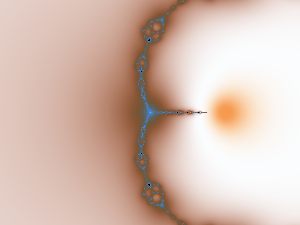 |
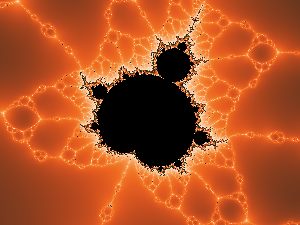 |
| original image | 50x zoom and slight color palette rotation |
A Mandelbrot - looking shape has appeared! This is an interesting situation. The region with the fancy colors, like the divergent region for the Mandelbrot equation, is a CONVERGENT region (actually basins of attraction), and the black interior is a region that does not converge to zero, but instead the z values cycle through orbits with absolute values that never blow up to infinity. In addition to regions which are basins of attraction for some root to the equation, there are also regions like the classic Mandelbrot set. Just like with the Mandelbrot set, the image provides a map to many Julia sets. The next image is an example:

Besides Newton's Method there are other formulas for finding roots of complex equations. Some examples which have been used in various UltraFractal formulas include the Householder, Halley and Schröder Methods.