Mathematics of Hyperbolic Tessellation Fractals

Hyperbolic geometry is a non-Euclidean geometry developed independently by Nikolai Lobachevski and Farkas Bolyai. In hyperbolic geometry the sum of the angles of a triangle is always less than 180°. Henri Poincaré developed a method to represent infinite two-dimensional hyperbolic space on a disc. The Poincaré disc is a map of the entire hyperbolic plane.

In two dimensions, tessellation is the regular tiling of a surface using polygons. In the Euclidian plane there are exactly 3 allowed tessellations using regular polygons. There are symbolized by {6,3}, {4,4} and {3,6}. The first number in the symbol is the number of sides of the polygon and second is the number of polygons surrounding each vertex. The symbol is called a Schläfli symbol. Consider {n,k}. It can be shown that if

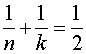
the tessellation is Euclidian, and only the three previously mentioned configurations satisfy the equation. On the hyperbolic plane, the relationship is

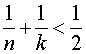
and so many combinations of n and k provide regular tessellations. If the hyperbolic tessellation is mapped to the Poincaré disc a very pleasing, fractal-like object is obtained, especially if the polygon contains an artistic image.

Hyperbolic geometry created new possibilities for producing artistic tessellations, which is illustrated in the art of M. C. Escher.

An example, which is a {4,5} tessellation created in Ultra Fractal is shown below. The image came from a floral design on a pottery tile. Notice that as the tessellation approaches the border of the disk, the image repeats in finer and finer detail, approaching infinity.