Mathematics of Fractals with More Than Two Dimensions

JuliaBrots

Consider the equation

z_n+1 = z²_n + c

Each value of the complex constant c will generate a different sequence. With a graph with the X axis (real axis) covering the range -2.5 to 1.5 and the Y axis (imaginary axis) covering the range -1.5 to 1.5 the Mandelbrot Set image is obtained. (See Mathematics of Divergent Fractals). Now assign to c a point in the Mandelbrot set or its immediate surrounding region. This will be called a Julia set index. On a new graph ranging from -2 to 2 on the real X axis and ranging from -1.5 to 1.5 on the imaginary Y axis, choose a point on the graph and assign it to z₀. Now iterate the equation. Do this for every point on the graph, using the same value of c for all iterations. This will generate a Julia set for the point c. 

Clearly, c can also be treated as a variable, and so the above equation has 4 dimensions, two for the real and imaginary parts of z, and two for the real and imaginary parts of c. This 4 dimensional object was named a JuliaBrot by Mark Peterson, one of the original developers of the Fractint fractal generating software. By holding one of the dimensions constant a 3D JuliaBrot can be generated. The three images below illustrate a JuliaBrot generated with Fractint and UltraFractal. For these images c_real is held constant and c_imag is the z axis. The UltraFractal JuliaBrot code was written by this author and is in the public UltraFractal library.

Fractint	UltraFractal distance mode	UltraFractal Raytrace mode
Iterations = 150 creal = 0.25 cimag = 2.0 to -2.0

The following two JuliaBrots, using the Ikenaga and Phoenix fractals, were also created in UltraFractal.

Ikenaga Iterations = 128 4th-dimension: cimag cimag = 0.09	Phoenix iterations = 128 4th-dimension: creal creal = 0.56667

Quaternions and Hypercomplex Fractals

Complex numbers, which can be graphed in 2-dimensions, can be generalized to 4-dimensions. The two most common generalizations are quaternions and hypercomplex numbers. Quaternions are widely used in physics.

Complex: h = a + bi

Quaternion/Hypercomplex: h = a + bi + cj + dk

where i, j and k are "imaginary" numbers. Quaternions and hypercomplex numbers have different rules for arithmetic that follow from the properties of their "imaginary" components.

For Quaternions:

ij = k    ji = -k
jk = i    kj = -i
ki = j    ik = -j
ii = jj = kk = -1
ijk = -1

For Hypercomplex  numbers:

ij = ji = k
jk = kj = -i
ki = ik = -j
ii = jj = -kk = -1
ijk = 1

As a result of these properties, multiplication is not commutative for quaternions (h₁*h₂ is not equal to h₂*h₁), but is so for hypercomplex numbers. For hypercomplex numbers, division is not always defined. This author has developed a complete library of transcendental functions for both quaternions and hypercomplex numbers for use with UltraFractal 5.  

Using the equation

z_n+1 = z²_n + c

but now with quaternion or hypercomplex numbers, the graphing of z now requires four dimensions. The next two images were generated with Fractint using hypercomplex or quaternion numbers.

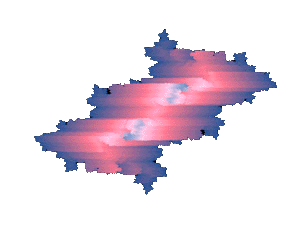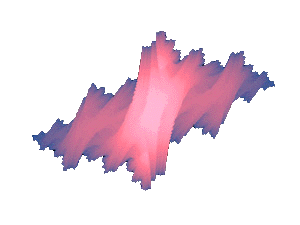Hypercomplex Iterations = 256 cr = -0.5; ci = -0.5 cj = 0.0; ck = 0.0 4th-dimension: zj	Quaternion Iterations = 256 cr = -0.5; ci = -0.5 cj = 0.0; ck = 0.0 4th-dimension: zj

The next image, which shows considerably more complexity,  is a raytraced quaternion generated with UltraFractal.

Quaternion
Iterations = 15
c_r = -0.7; c_i = 0.65
c_j = 0.0; c_k = 0.0
4th-dimension: zk